Lapsed ja animeeritud matemaatika

Võtame punkti x,y.
Arvutame sellest lihtsa lineaarse teisendusega järgmise punkti:
x1 = a1 * x + b1 * y
y1 = a2 * x + b2 * y
Joonistame x,y ja x1,y1 vahele joone.
Kordame.
Imetleme.

Tekib hulk väga väga erinevaid süsteeme.
Nende käitumine on parameetrite väikeste muutuste puhul väga erinev.
Millalgi kõdub kõik nulli.
Millalgi lendab lõpmatusse.
Tekivad siksakid, "torud", igasugu tsüklid.

Panin parameetrid (a1..b2) samuti väikese sammuga muutuma ja animeerisin programmi ära.
Ilus!
Lapsed vaatasid tükk aega ja nuputasid kujunditele "selgitusi" välja.

Tehniliselt on see x1=, y1= umbes lineaarvõrrandisüsteem, mille saab osade parameetrite fikseerimisel teiste jaoks välja arvutada. Ilmselt tekivad tema lahendite lähedal järsud üleminekud "nullist lõpmatusse" jne.
a1 a2 b1 b2 peavad olema väikesed (-2...+2 vahel) ja nende abs väärtuste summa ei tohi olla suur. Punkt peab jääma "pendeldama".

Nii palju lusti nii lihtsast lineaarsest arvutusest!

Moraal laste jaoks:
Ka lihtne matemaatika võib olla sisult keeruline ja vormilt ilus.

Lihtne peegeldus
x1 = -y
y1 = x
ehk a1 = 0, b1 = -1, a2 = 1, b2 = 0 annab ruudu:

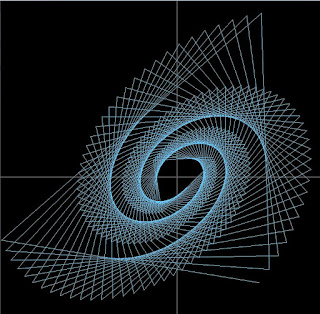
a1 = 1, a2 = 0.03, b1 = -0.03, b2 = 0.995 ehk "x ja y muutuvad mõlemad vähe" annab spiraali:

a1 = 0.2, a2 = -1, b1 = 1, b2 = 0:

-0.9, -1, 0.9, -0.1:

-1, 1.95, 0, 0.95: